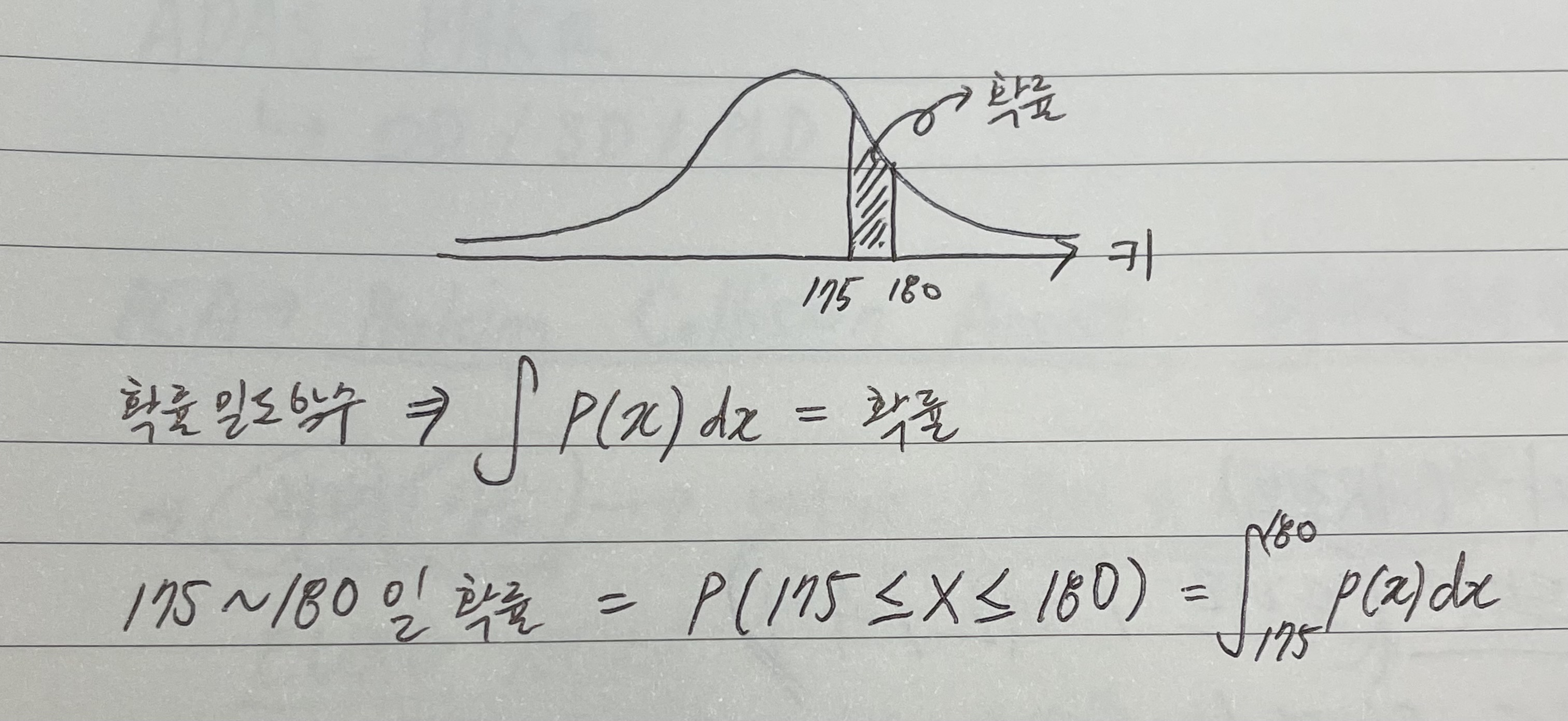확률과 라이클리후드(Likelihood)는 통계에서 많이 등장하지만, 그 차이를 구분하는 것이 헷갈릴 수 있습니다.
이 글에서는 확률과 라이클리후드의 차이를 쉽게 설명하고, 최대우도추정(MLE)이 무엇인지 알아보겠습니다.
Likelihood란 무엇인가?
먼저 사전적으로 "Likelihood"는 '어떤 일이 일어날 가능성'을 의미합니다. 하지만 통계에서 likelihood는 조금 다른 의미를 가지고 있습니다. 보통 Probability(확률)과 함께 다뤄지는데, 이 둘을 구분해보겠습니다.
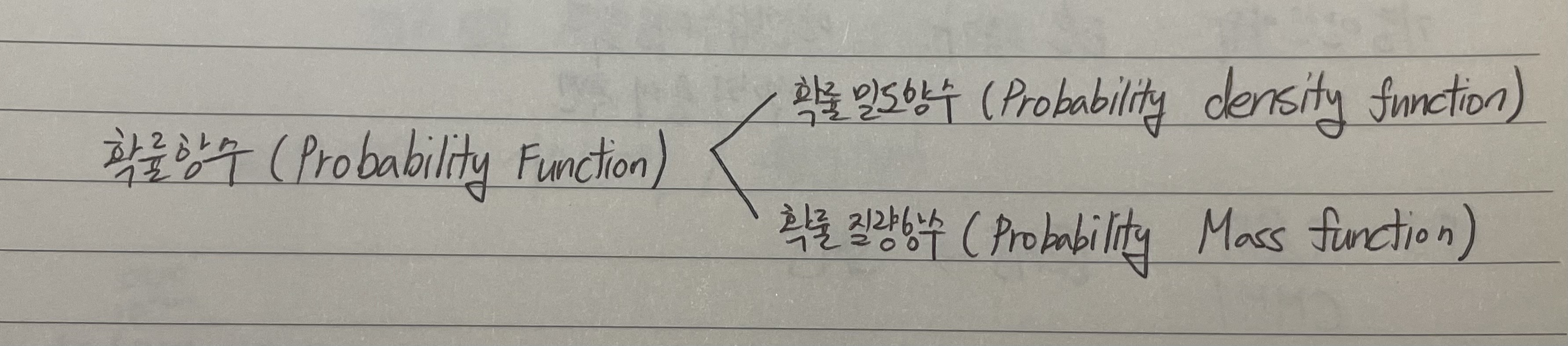
- 확률 (Probability): 어떤 사건이 일어날 가능성을 말합니다. 예를 들어, 특정 아이가 키가 클 확률 또는 카지노 게임에서 이길 확률을 생각해볼 수 있습니다.
- 가능도 (Likelihood) : 관측된 사건이 고정된 상태에서 확률 분포가 변화될 때, 확률을 나타냅니다. 즉, 데이터를 바탕으로 여러개의 확률분포를 적용하여 해당 확률 분포가 적합한지를 추정하는 데 사용됩니다. 식은 아래와 같습니다.

Likelihood
위의 식을 좀더 쉽게 이해하기 위해, 아래 식을 이해하면 좋습니다.

여기서 θ는 확률 분포를 구성하는 parameter(매개변수)를 의미합니다.
쉽게 말해, 특정 확률 분포의 성질을 정의하는 숫자들이라고 생각하면됩니다.
예를 들어, 확률분포가 정규분포를 따른다면 "θ"는 parameter는 평균 μ와 표준편차 σ가 됩니다.
따라서 위의 식은 likelihood는! 데이터 x일 때, 가정한 확률분포(예로 정규분포)의 확률값( P(x∣θ) )을 모두 곱한 값 (Π)이 됩니다.
예시 :
아래와 같이 데이터 x = {1,4,5,6,9} 가 주어졌을 때, 우리는 이 데이터를 가장 잘 설명할 수 있는 확률밀도함수(PDF)를 찾고자 합니다. 아래 그림처럼 여러 개의 PDF가 있을 수 있는데, 그 중에서 Likelihood 값이 가장 큰 확률밀도함수가 주황색 그래프입니다. likelihood값이 더 큰 확률밀도함수(PDF)는 주황색이 되겠죠.

이런 식으로, likelihood가 최대가 되는 확률밀도함수를 찾는 방법이 최대우도추정법 ( MLE, Maximum Likelihood Estimation) 입니다.
reference
[개념 정리] Likelihood 와 Probability
사전에서 Probability를 '확률', Likelihood는 '가능도, 가능성'라고 합니다. 이 단어의 구별이 잘 되지 않습니다. 한국어로 '확률'은 '어떤일이 일어날 가능성'을 나타냅니다. Likelihood도 '어떤일이 일어
xoft.tistory.com
'프로그래밍 > 수학' 카테고리의 다른 글
| What is the Natural Constant e (Exponential)? (0) | 2025.03.15 |
|---|---|
| Hungarian Algorithm: What Is It? (0) | 2025.03.12 |
| 조건부 종속성(Conditional Dependence)이란? 쉽게 이해해보기 (3) | 2024.10.03 |
| 확률 변수 & 확률 함수 (5) | 2024.09.30 |
| 내적 (Dot product) (3) | 2024.09.29 |