✅ tasks.json이란?
tasks.json은 **빌드 작업(컴파일 명령)**을 정의하는 파일
{
"label": "build C file", // 작업 이름
"type": "shell", // 터미널에서 실행할 명령
"command": "gcc", // 실행할 명령어 (예: gcc)
"args": [ // 명령어 뒤에 붙는 인자들
"-g", // 디버깅 정보 포함
"${file}", // 현재 열려있는 파일
"-o", "${fileDirname}\\${fileBasenameNoExtension}.exe" // 출력 exe 파일 이름
]
}여기서 ${file}, ${fileDirname} 같은 것들은 VS Code의 변수
- ${file}: 현재 열려 있는 파일 전체 경로
- ${fileDirname}: 파일이 있는 폴더
- ${fileBasenameNoExtension}: 파일 이름(확장자 제외)
✅ launch.json이란?
launch.json은 디버깅 환경을 설정하는 파일
F5를 눌렀을 때 어떤 프로그램을 실행해서 디버깅할지를 여기서 정의
{
"name": "Debug", // 디버그 설정 이름
"type": "cppdbg", // C++ 디버거 사용
"request": "launch", // launch or attach
"program": "${fileDirname}\\${fileBasenameNoExtension}.exe", // 실행할 프로그램
"cwd": "${fileDirname}", // 작업 디렉토리
"externalConsole": true, // 외부 콘솔에서 실행 (cmd)
"MIMode": "gdb", // GDB 디버거 사용
"miDebuggerPath": "gdb" // GDB 경로
}miDebuggerPath는 MinGW-w64에 포함된 gdb.exe 경로여야 해. 예: C:\\mingw-w64\\mingw64\\bin\\gdb.exe
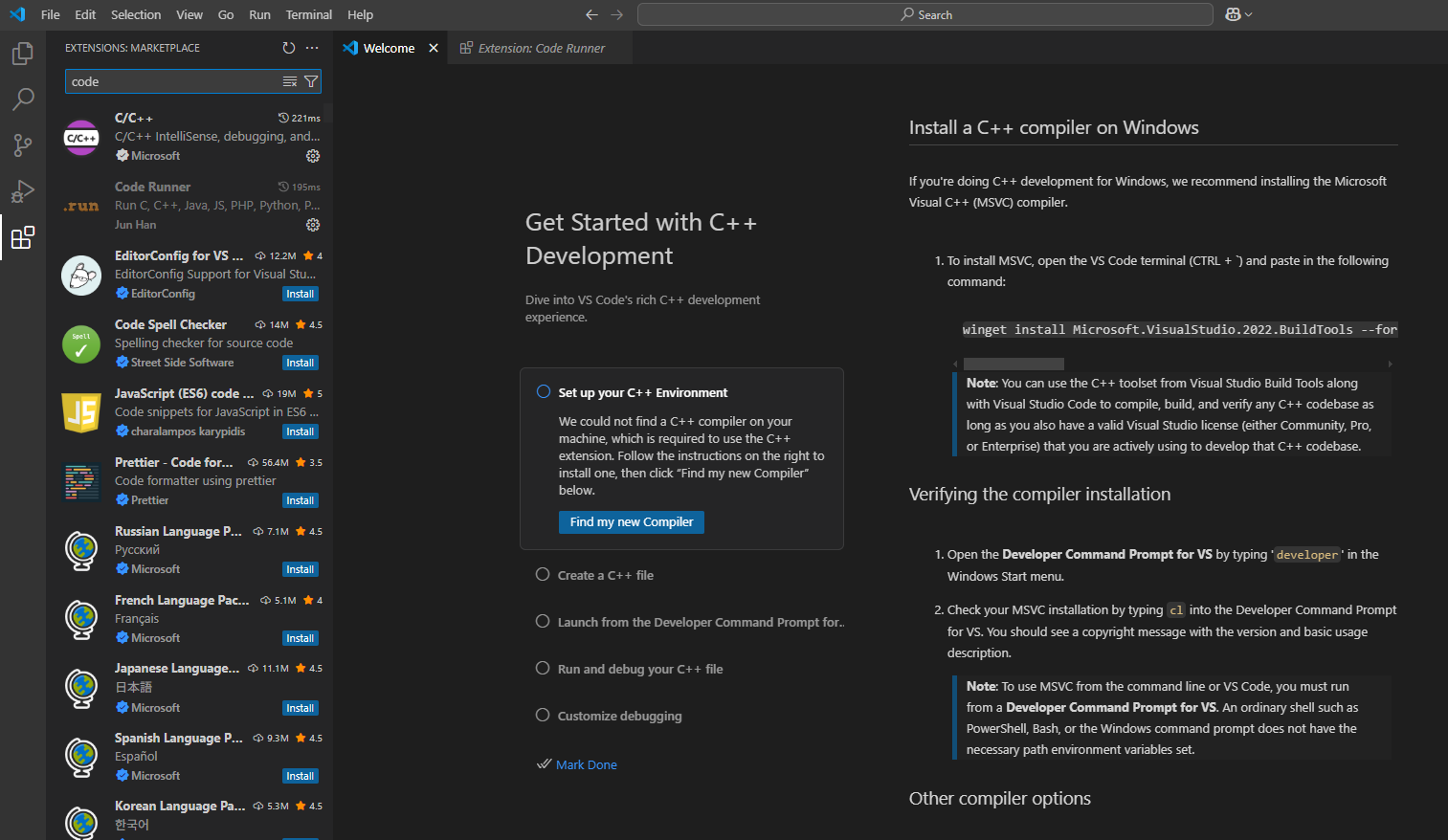
🔧 VS Code 직접 설정 튜토리얼 정리
| 설정 | 파일역할 | 예 |
| tasks.json | 컴파일 명령어 정의 | gcc hello.c -o hello.exe |
| launch.json | 디버깅 실행 방법 정의 | gdb hello.exe 디버깅 시작 |
🤔 CMake랑 뭐가 달라?
✅ VS Code 설정 방식 특징
- tasks.json과 launch.json을 직접 써야 함
- 프로젝트 구조가 단순할 때는 빠르게 사용 가능
- 자동화가 부족하고, 대형 프로젝트에서는 유지가 어려움
✅ CMake 특징
- CMake는 크로스 플랫폼 빌드 시스템 생성기
- CMake 파일(CMakeLists.txt)을 만들어 프로젝트 전체 빌드 과정을 자동화
- Makefile, Ninja, Visual Studio 솔루션 등 다양한 빌드 시스템을 생성 가능
- 프로젝트 구조가 복잡할수록 유리함 (라이브러리 여러 개, 서브디렉토리 등)
🔍 비교 요약
| 항목 | VS Code 설정 (tasks.json/launch.json) | CMake |
| 사용 대상 | 간단한 프로젝트 | 중/대형 프로젝트 |
| 설정 복잡도 | 낮음 | 처음은 조금 높음 |
| 자동화 정도 | 수동 | 자동화 |
| 플랫폼 지원 | VS Code 내에서만 작동 | 플랫폼 독립 (Windows, Linux, macOS 등) |
| 유지보수 | 직접 경로 수정 필요 | 변수/설정으로 유연하게 관리 |
💬 언제 CMake를 써야 할까?
- 프로젝트에 파일이 3개 이상이 되거나, 헤더/소스가 분리되기 시작하면 CMake를 고려.
- g++ main.cpp module1.cpp module2.cpp 이런 명령어가 길어지기 시작하면 이제는 CMake가 필요할 때.
'프로그래밍 > vscode' 카테고리의 다른 글
| 윈도우에서 VS Code로 C/C++ 개발 환경 설정하기 (2025년 최신 가이드) (0) | 2025.04.20 |
|---|---|
| VScode란? (0) | 2025.04.01 |