천천히 꾸준히

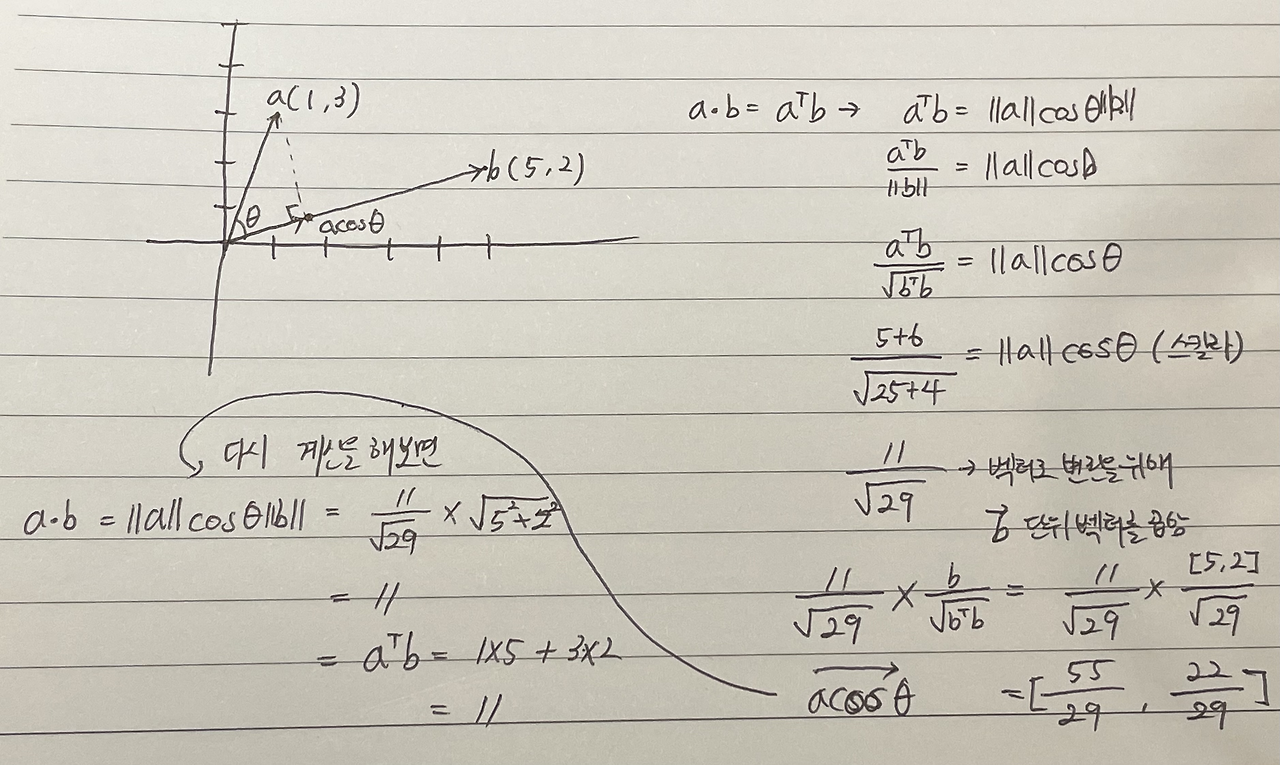
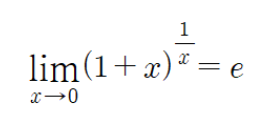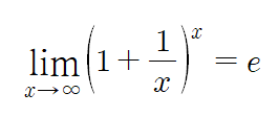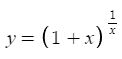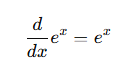When studying statistics or machine learning, you often encounter the term variance. But what exactly does it mean, and why is it important? In this post, we'll break it down in simple terms and explore its significance in data analysis and machine learning.

Understanding Variance

Variance is a measure of how much a set of numbers deviates from their mean (average). In simpler terms, it tells us how spread out the values in a dataset are.

Imagine you have test scores of five students:

85, 90, 95, 100, 105

If the scores were all the same, there would be no variance. However, since they differ, we can calculate variance to measure this spread.

The formula for variance (σ²) is:

where:

• N = number of data points
• xᵢ = each individual data point
• μ = mean (average) of the data

Step-by-Step Example

Let’s calculate the variance of our test scores:

1. Find the mean (μ):
   

   

   
   
2. Calculate each deviation from the mean and square it:
   

   

   
   
   
3. Find the average of these squared differences:
   

So, the variance of this dataset is 50.

Why is Variance Important?

1. In Statistics

Variance helps describe data distribution. A low variance means the data points are close to the mean, while a high variance means they are spread out. This is useful in analyzing trends and making predictions.

2. In Machine Learning

In machine learning, variance is critical when evaluating model performance:

• High variance: The model is too sensitive to training data and may not generalize well (overfitting).
• Low variance: The model is too simple and may fail to capture important patterns (underfitting).

Variance vs. Standard Deviation

Variance is often compared to standard deviation (σ), which is simply the square root of variance:

Standard deviation is useful because it is in the same units as the original data, making it easier to interpret.

Conclusion

Variance is a fundamental concept in statistics and machine learning. It helps us understand data distribution and plays a crucial role in model evaluation. Whether you're analyzing test scores or training AI models, understanding variance will improve your data interpretation skills!

Reference

• Original Blog Post

While reading a research paper, I came across a concept that always confuses me: the dot product. Every time I encounter it, I find myself searching for explanations, only to forget them later. This time, I am determined to understand and remember it!

What is the Dot Product?

According to Wikipedia, the dot product is:

"An operation that takes two vectors in Euclidean space and returns a real scalar. In physics, the concept of scalar multiplication helps determine the work done by a force on an object along a displacement."

Okay... but what does that actually mean?

After watching some YouTube videos, particularly from Hefpenheim, I found a more intuitive explanation:

• The dot product is a way to measure how similar two vectors are.
• If the dot product is large, the vectors are in a similar direction.
• If it is zero, the vectors are perpendicular.
• If it is negative, the vectors are in opposite directions.

Still not fully clear? Let’s break it down mathematically.

Mathematical Definition

The dot product is denoted by "⋅" and is calculated as:

where:

• a and b are vectors,
• ||a|| and ||b|| are their magnitudes (lengths), and
• θ is the angle between them.

Example Calculation

Imagine we have two vectors a and b. The term represents the projection of a onto b. This means the dot product gives us a way to measure how much one vector influences another along a given direction.

For example, if , the vectors are perfectly aligned, and the dot product is at its maximum value. If , the vectors are perpendicular, meaning they have no influence on each other in terms of direction.

Key Takeaways

1. The dot product helps measure the similarity between two vectors.
2. It produces a scalar value, not another vector.
3. The formula to remember is:

Now, next time I see "dot product" in a paper, I won’t have to search for it again!

References

• YouTube: Understanding the Dot Product

When studying the Hungarian algorithm, you often encounter terms like matching and vertex cover. But what exactly do they mean, and why do they appear so frequently?

Understanding Vertex Cover

A vertex cover is a set of vertices in a graph that covers all edges. In other words, every edge in the graph must be incident to at least one vertex in the vertex cover.

But wait—what exactly are vertices, edges, and graphs? Let’s break it down.

What is a Graph?

A graph is a structure consisting of vertices (nodes) connected by edges (lines). Here’s a simple way to visualize it:

• Vertex (Node): A point where edges meet.
• Edge (Line): A connection between two vertices.

For example, the following graph has 6 vertices and 5 edges:

(Insert a simple graph illustration with labeled vertices and edges)

Back to Vertex Cover

Now that we understand what a graph is, let’s return to our original definition of a vertex cover:

A vertex cover is a set of vertices that includes at least one endpoint of every edge in the graph.

To make it even simpler: If you remove all edges that are connected to the selected vertices, no edges remain.

Example of a Vertex Cover

In the graphs below, the red-colored vertices represent a vertex cover. Selecting these vertices ensures that every edge in the graph is covered:

(Insert example graphs with highlighted vertex covers)

Why is Vertex Cover Important?

The concept of vertex cover is fundamental in graph theory and is closely related to matching problems and the Hungarian algorithm. Understanding it will help you grasp advanced topics more easily, especially in optimization problems.

If you revisit the Hungarian algorithm after understanding vertex cover, other explanations and resources will make much more sense!

References

• Graph Basics
• Hungarian Algorithm & Vertex Cover
• Matching and Vertex Cover

In mathematics, the natural constant e plays a crucial role. Like other fundamental mathematical constants, e is indispensable in many areas of mathematics:

• 1: The identity element for multiplication
• 0: The identity element for addition
• π: The ratio of a circle’s circumference to its diameter
• e: The base of the natural logarithm

But what exactly is e?

Defining e

The number e can be understood as "the value obtained when you raise (1 + a very small number) to an infinitely large power."

Mathematically, this is expressed as:

As x grows infinitely large, the value of the expression approaches e.

Approximate Value of e

Since e is an irrational number and a transcendental number, it cannot be exactly expressed as a finite decimal. However, its approximate value is:

e ≈ 2.718281828

Simply put, e is a natural constant, approximately 2.71828, and it results from raising (1 + an infinitely small number) to an infinitely large power.

Understanding e with a Graph

To better understand e, let's look at the graph of the function:

As x approaches infinity, the function’s value converges to e ≈ 2.71828. Conversely, as x decreases toward negative values, the function grows exponentially.

This property makes e fundamental in exponential growth and decay models.

Why is e Important?

e is more than just a number. It appears in many crucial areas of mathematics and science:

1. The Base of the Natural Logarithm:
   • The natural logarithm (ln) is defined using e, making it essential in logarithmic functions.
2. Compound Interest and Growth Models:
   • e is used in financial models, population growth, and radioactive decay calculations.
3. Calculus and Differential Equations:
   • Many fundamental formulas in calculus involve e, especially in differentiation and integration.

Because of these properties, e is one of the most important mathematical constants.

Additional Explanation

One fascinating fact about e is that it appears naturally in situations involving continuous growth. For example, if you continuously compound interest on an investment, the final amount can be calculated using e.

Additionally, in calculus, the function e^x has the unique property that its derivative is itself:

This makes e the foundation of many mathematical models describing real-world phenomena.

References

• Naver Knowledge Encyclopedia
• Desmos Graphing Calculator