In mathematics, the natural constant e plays a crucial role. Like other fundamental mathematical constants, e is indispensable in many areas of mathematics:
- 1: The identity element for multiplication
- 0: The identity element for addition
- π: The ratio of a circle’s circumference to its diameter
- e: The base of the natural logarithm
But what exactly is e?
Defining e
The number e can be understood as "the value obtained when you raise (1 + a very small number) to an infinitely large power."
Mathematically, this is expressed as:
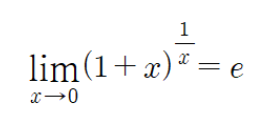
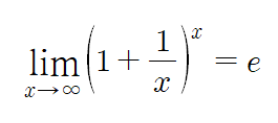
As x grows infinitely large, the value of the expression approaches e.
Approximate Value of e
Since e is an irrational number and a transcendental number, it cannot be exactly expressed as a finite decimal. However, its approximate value is:
e ≈ 2.718281828
Simply put, e is a natural constant, approximately 2.71828, and it results from raising (1 + an infinitely small number) to an infinitely large power.
Understanding e with a Graph
To better understand e, let's look at the graph of the function:
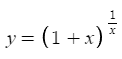
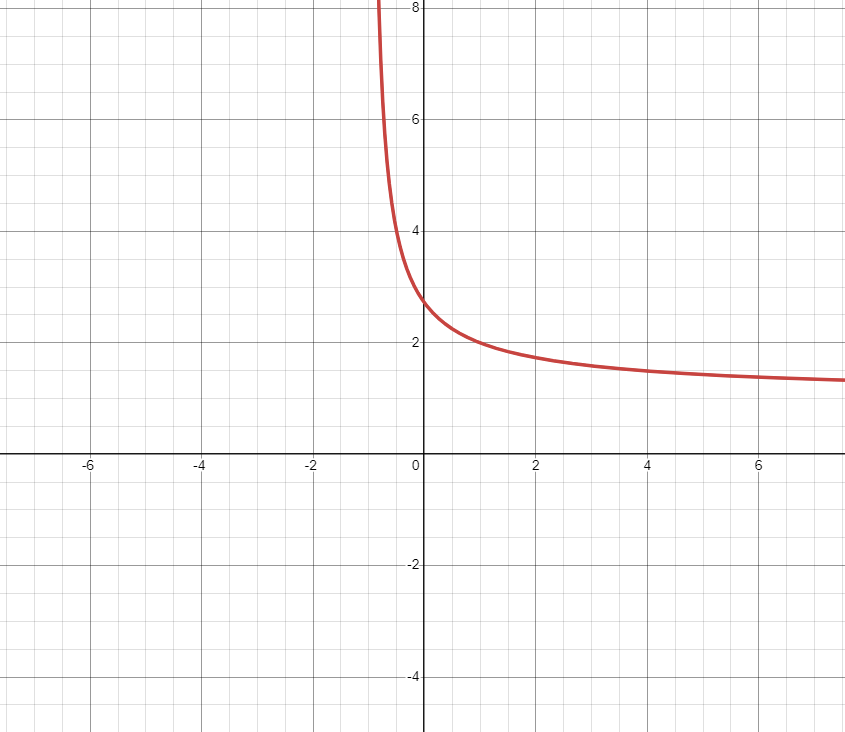
As x approaches infinity, the function’s value converges to e ≈ 2.71828. Conversely, as x decreases toward negative values, the function grows exponentially.
This property makes e fundamental in exponential growth and decay models.
Why is e Important?
e is more than just a number. It appears in many crucial areas of mathematics and science:
- The Base of the Natural Logarithm:
- The natural logarithm (ln) is defined using e, making it essential in logarithmic functions.
- Compound Interest and Growth Models:
- e is used in financial models, population growth, and radioactive decay calculations.
- Calculus and Differential Equations:
- Many fundamental formulas in calculus involve e, especially in differentiation and integration.
Because of these properties, e is one of the most important mathematical constants.
Additional Explanation
One fascinating fact about e is that it appears naturally in situations involving continuous growth. For example, if you continuously compound interest on an investment, the final amount can be calculated using e.
Additionally, in calculus, the function e^x has the unique property that its derivative is itself:
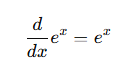
This makes e the foundation of many mathematical models describing real-world phenomena.
References
'프로그래밍 > 수학' 카테고리의 다른 글
| Understanding the Dot Product: A Simple Explanation (0) | 2025.03.19 |
|---|---|
| What is a Vertex Cover? (0) | 2025.03.18 |
| Hungarian Algorithm: What Is It? (0) | 2025.03.12 |
| Likelihood와 최대우도추정(MLE): 확률과 데이터의 관계 쉽게 이해하기 (1) | 2024.10.04 |
| 조건부 종속성(Conditional Dependence)이란? 쉽게 이해해보기 (3) | 2024.10.03 |